Halbwertszeit

Bei üblichen Diskussionen über die Halbwertszeit bleibt meist unklar, wann eine radioaktive Substanz denn nun „völlig weg“ ist.

Aufgrund aktueller Ereignisse wird in den Medien sehr viel über radioaktive Substanzen und deren Zerfall gesprochen.

Bekanntermaßen wird die Zerfallsgeschwindigkeit radioaktiver Substanzen mittels der Halbwertszeit 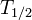$T_{1/2}$ angegeben. So liegt diese etwa für Iod-131 bei ca. acht Tagen oder für Plutonium-239 gar bei über 24.000 Jahren.

Warnung: Böswillige Mathematik voraus.

Diese Zeit gibt dabei nur an, nach welcher Zeit die Hälfte der ursprünglichen Substanzmenge 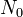$N_0$ zerfallen ist. Die verbleibende Menge 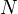$N$ nach einer Zeit $t$ ergibt sich durch

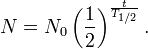
$N = N_0 \left(\frac{1}{2}\right)^\frac{t}{T_{1/2}}.$

Möchte man nun wissen, wann 99% der Ausgangsmenge „verschwunden“ ist, reicht dazu ein bisschen Rechnerei.

Es soll also nur noch 1% der Ausgangsmenge 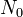$N_0$ vorhanden sein

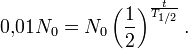
$0{,}01 N_0 = N_0 \left(\frac{1}{2}\right)^\frac{t}{T_{1/2}}.$

Hier kann man die Ausgangsmenge kürzen

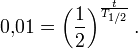
$0{,}01 = \left(\frac{1}{2}\right)^\frac{t}{T_{1/2}}.$

Um nun die gesuchte Zeit $t$ zu erhalten zu der nur noch 1% übrig ist, logarithmieren wir beide Seiten der Gleichung

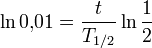
$\ln 0{,}01 = \frac{t}{T_{1/2}} \ln\frac{1}{2}$

und lösen nach $t$ auf:

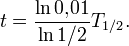
$t = \frac{\ln 0{,}01}{\ln 1/2} T_{1/2}.$

Ergebnis

Die Logarithmen kann man leicht mit dem Taschenrechner bestimmen und man erhält dann

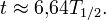
$t \approx 6{,}64 T_{1/2}.$

Das bedeutet nun also, dass man etwa die 6,6-fache Halbwertszeit warten muss, bis 99% der ursprünglichen Substanz zerfallen sind.

Das sollte man auch bei augenscheinlich kurzen Halbwertszeiten bedenken.